Gro Intelligence’s analytics provide valuable and actionable insights across agriculture, climate, and the economy.

Gro is the story of what on Earth is going on
We illuminate the interrelationships between the Earth's ecology and the global economy, so you can develop a holistic understanding of how your end-to-end business is impacted - and act on these insights. Curated by human intelligence and scaled through artificial intelligence, our system is built to give you the honest answers to your specific situation.
Food & Beverage
Optimize your supply chain and align to future scenarios
Seed and Fertilizer
Plan for marketing strategies around changing conditions
Financial Institutions
Manage risk and trade with a longer, more confident view
Public Sector
Monitor local and global food security and understand the effects of climate change
Grocery and Retail
Procure in the right regions, at the right price
Shipping
Forecast global grain movements across short- and long-term use cases
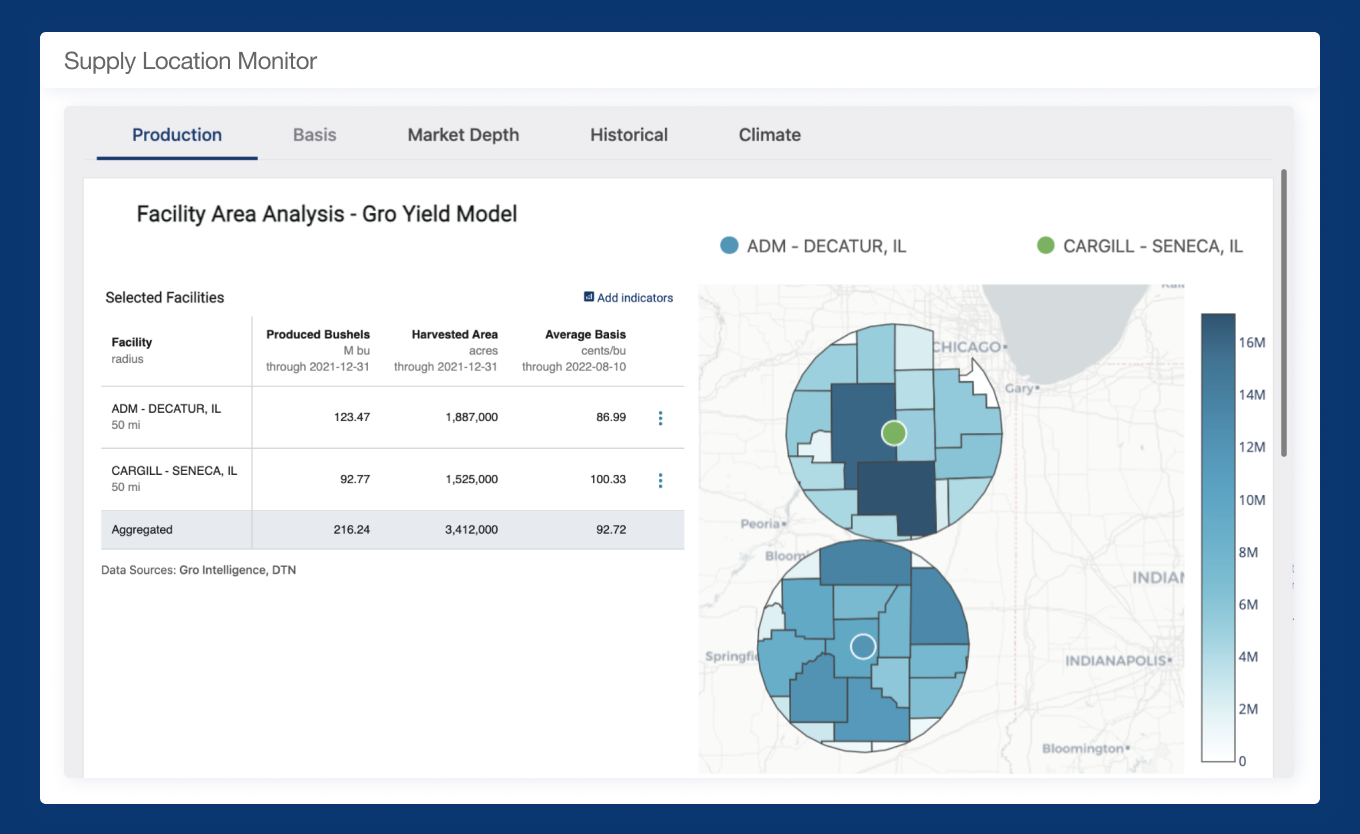
Inspiring confidence to get to the honest answer
Gro analytics and indices make agricultural, climate, and economic data actionable.
Working with customers to:
1.
Build sustainable supply chains
Evaluate similar regions for sourcing today and in future climate scenarios
2.
Plan for margin impact
Map historical and present availability and prices to chart impact
3.
Procure and trade with confidence
See inputs and methodology to build your own forecasts
4.
Mitigate risk
See around the corner, managing risks with a longer time horizon
5.
Map food availability
Use changes in balance sheets and climate scenarios to plan for access
6.
Monitor food security
Track the drivers of food insecurity to plan for national reserves or aid responses
Sign up for Gro Updates


 Search
Search